Стартовал второй этап нашего конкурса 2024/2025 учебного года!
Конкурс проводится в три этапа: с сентября по декабрь, с января по апрель и с мая по август. Дипломы и призы получат не только победители за весь год, но и победители каждого этапа. Приглашаем всех присоединиться и попробовать свои силы!

Задачи конкурса печатаются в каждом номере. Участвовать можно, начиная с любого тура. Победителей ждут дипломы журнала «Квантик», научно-популярные книги.
Конкурс ориентирован на школьников 5-8 классов, но и младшеклассники могут присылать решения. Вносите решения задач VIII тура, с которыми справитесь, не позднее 5 мая в систему проверки konkurs.kvantik.com (инструкция kvantik.com/short/matkonkurs), или высылайте по электронной почте matkonkurs@kvantik.com, либо обычной почтой по адресу: 119002, Москва, Б. Власьевский пер., д. 11, журнал «Квантик». В письме кроме имени и фамилии укажите город, школу и класс, в котором вы учитесь, а также обратный адрес.
Задачи и результаты конкурсов прошлых лет: 2023/2024, 2022/2023, 2021/2022, 2020/2021, 2019/2020, 2018/2019, 2017/2018, 2016/2017, 2016, 2015, 2014, 2013, 2012.
Желаем успеха!
VIII тур
Задача 36. (Александр Грибалко)
Назовём натуральное число троечным, если оно делится на 3 или содержит тройку в десятичной записи. Найдите хотя бы одно такое число N, что среди чисел от 1 до N ровно половина троечных.

Задача 37. (Иван Русских)
У Саши есть плоская коробка в виде клетчатого многоугольника, в которой лежат 5 шоколадок размером 1 × 5. Саша захотел упаковать шоколадки так, чтобы они не болтались (никакую нельзя подвинуть ни по горизонтали, ни по вертикали ни на одну клеточку). Оказалось, что тогда в коробку можно упаковать 2 шоколадки, а больше — не получается. Приведите пример такой коробки.

Задача 38. (Борис Френкин)
У мудрецов Пети, Васи и Тимы ко лбу прикреплены бумажки, на каждой из которых написано натуральное число. Известно, что сумма всех трёх чисел не больше 5. На вопрос «можешь ли ты назвать своё число» Петя ответил «нет», затем Вася ответил «нет», а затем Тима назвал своё число и обосновал ответ. Какое число было написано у Тимы?

Задача 39. (Сергей Костин)
Вася покрасил 131 клетку в квадрате 13 × 13 в синий цвет, а остальные клетки в зелёный. Верно ли, что Петя в любом случае сможет вырезать из этого квадрата двадцать целиком синих пентаминошек (не обязательно одинаковых)?

Задача 40. (Михаил Евдокимов)
В треугольнике ABC биссектриса угла A делит медиану, проведённую из вершины B, пополам. Какое наибольшее значение может иметь величина угла C?

VII тур
Задача 31. (Сергей Полозков)
Фигуру на рисунке разрежьте на две части и сложите из них правильный шестиугольник (все его стороны равны, и все углы тоже). Части можно поворачивать и переворачивать.


Задача 32. (Сергей Костин)
Замените снежинки в ребусе на различные цифры (от 0 до 9) так, чтобы получилось верное равенство. (Напомним, что натуральное число в нулевой степени считается равным 1.)


Задача 33. (Борис Френкин)
Вася испёк пирог в виде квадрата и отрезал от него треугольник так, что остался четырёхугольник. Затем он разрезал четырёхугольную часть на два треугольника. Какую долю от всего пирога составляет наибольшая из трёх получившихся частей? (Все разрезы прямолинейные.)

Задача 34. (Александр Перепечко)
В каждой клетке бесконечной клетчатой плоскости нарисована стрелка вверх, вниз, вправо или влево. Может ли оказаться так, что из каждой клетки в каждую есть путь, идущий по соседним клеткам согласно стрелкам?

Задача 35. (Александр Грибалко)
Пять спортсменов провели восемь забегов на разные дистанции; все всегда финишировали в разное время. Перед каждым забегом Петя делал прогноз, в каком порядке финишируют спортсмены, а потом записывал в блокнот, сколько позиций он угадал верно. В итоге оказалось, что каждое следующее число в блокноте отличается от предыдущего, а сумма всех восьми чисел равна 30. В скольких забегах Петя угадал все пять позиций?

VI тур
Задача 26. (Борис Френкин)
Маша, которая сейчас учится в школе, записала свою дату рождения в формате ДД.ММ.ГГ, использовав шесть различных цифр. Могла ли Маша родиться в один из зимних месяцев? Ответ объясните.

Задача 27. (Сергей Костин)
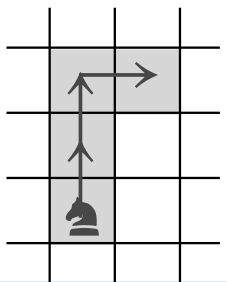
Петя ходит шахматным конём, не отрывая его от доски (то есть конь посещает и промежуточные клетки хода, см. пример на рисунке). Может ли Петя, начав с какой-то клетки, обойти конём всю доску 5×5, посетив каждую клетку ровно один раз?

Задача 28. (Михаил Евдокимов)
Вася называет натуральное число, состоящее из ненулевых цифр, красивым, если и произведение, и сумма его цифр делятся на 100. Найдите наименьшее красивое число и докажите, что меньше него красивых чисел нет.

Задача 29. (Николай Авилов)
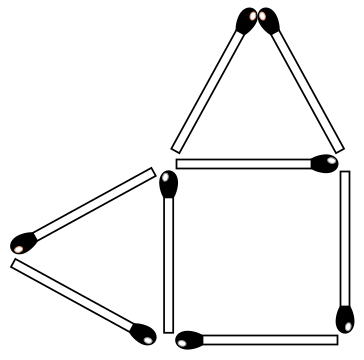
Из спичек сложен квадрат, а на двух его сторонах из спичек построены равносторонние треугольники. Получился невыпуклый шестиугольник. Переложите две спички внутри него так, чтобы он разделился на две части, равные по форме и по размеру. (Спички не должны выходить за пределы шестиугольника, их нельзя ломать, нельзя накладывать друг на друга.)

Задача 30. (Максим Прасолов)
Четверо ребят получили от воспитательницы по игрушке. Потом она собрала эти четыре игрушки и снова раздала ребятам так, что каждый получил ту игрушку, которой у него до этого не было.
а) Верно ли, что вне зависимости от того, как были выданы игрушки до этого, воспитательница сможет собрать игрушки и раздать их в третий раз так, чтобы каждый получил новую?
б) А в четвёртый раз? Ответ объясните.

V тур
Задача 21. (Максим Прасолов)
Замок имеет форму правильного треугольника. Барон хочет расставить часовых на стенах замка так, чтобы каждая точка вне замка была в поле зрения часовых. Хватит ли шести часовых, если часовой видит всё в пределах угла 60°, причём замок не должен загораживать обзор? В одной точке можно располагать несколько часовых.

Задача 22. (Борис Френкин)
Вася в течение 7 дней подряд решал задачи (не меньше чем по одной), причём в каждый следующий день он решал на 1 задачу больше, с единственным исключением: в воскресенье Вася решил столько же задач, сколько и в субботу. Всего он решил 24 задачи. Сколько задач Вася решил в среду?

Задача 23. (Александр Грибалко)
Набор домино состоит из 28 различных прямоугольников 1×2, в клетках которых поставлено от 0 до 6 точек. Петя сложил все доминошки в произвольном порядке в кольцо так, что получилась прямоугольная рамка толщиной в клетку доминошки. Затем Вася склеил все доминошки по соседним сторонам, а потом разрезал каждую доминошку на две половинки. Могло ли оказаться, что полученные Васей доминошки тоже образуют полный набор?

Задача 24. (Николай Авилов)
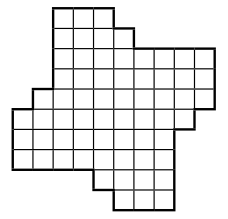
Фигуру-«вертушку», изображенную на рисунке, разрежьте на четыре равные (и по форме, и по размеру) части так, чтобы из них можно было сложить квадрат, без наложений и просветов.

Задача 25. (Сергей Костин)
На столе лежат шкатулки — 7 вверху и 7 внизу так, как на рисунке. В одной из шкатулок находится Волшебный цветок. Если открыть эту шкатулку, то начинает играть вальс. Если открыть шкатулку, в которой нет Волшебного цветка, но он находится в одной из соседних шкатулок (слева, справа, сверху или снизу), то звенит колокольчик. Какое наименьшее количество шкатулок надо открыть, чтобы точно понять, в какой шкатулке находится Волшебный цветок?


IV тур
Задача 16. (Ксения Пахомова)
Квантик написал на доске выражение, состоящее из двоек, знаков «+» и «×» и, возможно, скобок. Его значение равно 24. Ноутик заменил в этом выражении все знаки «+» на знаки «×», а все знаки «×» на знаки «+». Могло ли оказаться, что значение нового выражения тоже равно 24?

Задача 17. (Сергей Шамсутдинов)
Известно, что пятизначное число abcde делится на 41. Его последнюю цифру удалили и поставили в начало. Докажите, что полученное число eabcd тоже делится на 41.

Задача 18. (Сергей Полозков)
Разрежьте равносторонний треугольник на шесть равных четырёхугольников. Четырёхугольники равны, если их можно совместить наложением (возможно, с переворотом).

Задача 19. (Георгий Караваев)
В комнате находится 50 лампочек. К каждой лампочке подсоединены два выключателя, каждый либо включен, либо выключен. Лампочка горит только тогда, когда оба выключателя, подсоединённых к ней, включены. Сначала в комнате горело 15 лампочек, а когда все 100 выключателей переключили, стало гореть 24 лампочки. Сколько выключателей теперь надо переключить, чтобы зажглись все лампочки?

Задача 20. (Фёдор Ивлев)
Федя разложил перед собой 16 лотерейных билетов и продаёт их по 1000 рублей за каждый. Два из них выигрышные — купивший получит стоимость билета и ещё 1000 рублей выигрыша. Федя сегодня добрый, и за 100 рублей ему можно задать любой вопрос, который допускает ответ «да» или «нет», и он честно на него ответит. Можно ли, задав несколько вопросов, гарантированно заработать
а) 1200 рублей;
б) 1300 рублей?

III тур
Задача 11. (Михаил Леляков)
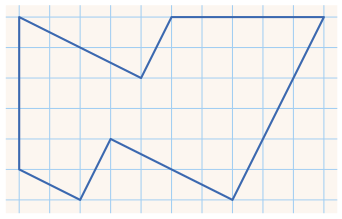
Разрежьте фигуру на рисунке на 2 равные (и по форме, и по размеру) части.

Задача 12. (Николай Авилов)
Квадрат 3×3 сложен из квадратных фишек 1×1, пронумерованных числами от 1 до 9. Изначально фишки лежат так, как на рисунке слева. Любые четыре фишки, образующие квадрат 2×2, можно поворачивать вокруг его центра на угол, кратный 90 градусам. Можно ли с помощью нескольких таких поворотов получить расположение, в котором фишки расположены так, как на рисунке справа?


Задача 13. (Игорь Акулич)
Квадраты последовательных натуральных чисел 13 и 14 записываются одними и теми же цифрами, но в разном порядке: 169 и 196. Существуют ли три последовательных натуральных числа, обладающих тем же свойством?

Задача 14. (Георгий Караваев)
Из клетчатой скатерти со стороной клетки 1 вырезали прямоугольник со сторонами, параллельными сторонам клеток, как на рисунке.
Суммарная площадь белой части прямоугольника равна 10. Найдите его периметр.


Задача 15. (Михаил Евдокимов)
Миша смотрел «Что? Где? Когда?» и выписывал счёт, начиная с 0:0 и до конца игры (в каждом раунде разыгрывается одно очко; игра заканчивается, когда зрители или знатоки наберут 6 очков). Если у зрителей было больше очков, Миша делал запись синей ручкой, если очков было больше у знатоков — красной ручкой, а если была ничья – зелёной. Могло ли оказаться, что красных, синих и зелёных записей было поровну?

II тур
Задача 6. (Михаил Евдокимов)
Квантик умеет выкладывать из спичек цифры по образцу как на картинке. Он выложил на столе перед собой некоторое число, не начинающееся и не заканчивающееся на 0. Ноутик посмотрел на это число с другой стороны стола. Могло ли оказаться, что число, которое видит Квантик, ровно в 8,5 раз больше числа, которое видит Ноутик?


Задача 7. (Михаил Евдокимов)
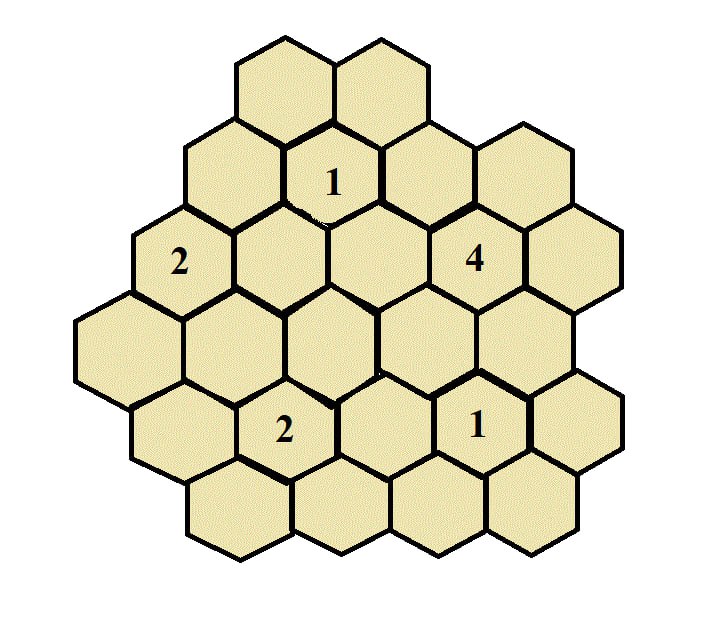
В некоторых пустых сотах указано, сколько соседних по стороне сот заполнено мёдом. Сколько всего сот заполнено мёдом?

Задача 8. (Борис Френкин)
На острове 30 жителей, каждый либо правдолюб (всегда говорит правду), либо лжец (всегда лжёт). Каждый знает про всех, кто есть кто. Островитяне встали в круг, и каждый сказал про соседа справа, правдолюб он или лжец, а потом сказал это про соседа слева. Может ли быть, что никто не сказал дважды одно и то же?

Задача 9. (Geometry Snacks)
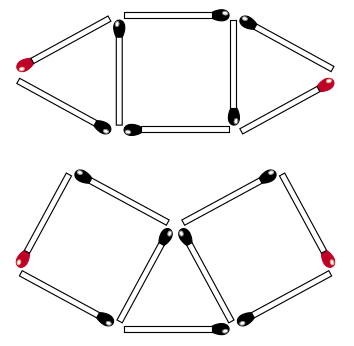
У какой из спичечных фигур расстояние между красными точками больше – у верхней или у нижней? Спички считайте одинаковыми и очень тонкими.

Задача 10. (Михаил Евдокимов)
Есть шахматная доска 8×8. За один ход можно выбрать любой клетчатый квадрат 2×2, 3×3 или 4×4 и изменить цвет четырёх его угловых клеток на противоположный. Можно ли
a) Сделать доску полностью белой?
б) Сделать какие-то две соседние по стороне клетки чёрными, а остальные клетки — белыми?
Приведите алгоритм действий или докажите, что такое невозможно.

I тур
Задача 1. (Татьяна Казицына)
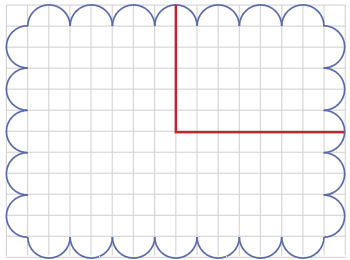
На рисунке вы видите печенье и пример, как сделать разрез по линиям сетки, чтобы отделить четверть (по площади). Можно ли от такого же печенья отрезать четверть (по площади) иначе — так, чтобы разрез шёл по линиям сетки и оказалcя короче, чем в примере?

Задача 2. (Михаил Евдокимов)
Дан треугольник, два угла которого равны 25° и 80°. Докажите, что в нём биссектриса какого-то угла и одна из трисектрис какого-то угла перпендикулярны друг другу. (Напоминание: биссектриса делит угол пополам, трисектриса отрезает треть угла; сумма углов любого треугольника равна 180°.)

Задача 3. (Михаил Евдокимов)
Фокусник взял две колоды по 52 карты в каждой и построил на столе треугольный карточный домик с наибольшим числом этажей. Сколько карт у него осталось на руках? На рисунке для примера показаны карточные домики в 2 этажа (из 7 карт) и в 3 этажа (из 15 карт).

Задача 4. (Николай Осипов и Аркадий Скопенков)
Даны целые числа

Задача 5. (Сергей Дориченко)
У Пети есть набор из трёх белых гирек массами 101 г, 102 г и 103 г, и такой же набор из трёх чёрных гирек. Массы на гирьках не написаны, а на вид нельзя понять, какая гирька какой тяжелее. Петя хочет разбить гирьки на пары одинаковых по массе. Как ему сделать это за два взвешивания на чашечных весах со стрелкой, показывающих, какая чаша перевесила и на сколько грамм?


