Приглашаем принять участие в нашем конкурсе 2025/2026 учебного года!
Конкурс проводится в три этапа: с сентября по декабрь, с января по апрель и с мая по август. Дипломы и призы получат не только победители за весь год, но и победители каждого этапа.

Задачи конкурса печатаются в каждом номере. Участвовать можно, начиная с любого тура. Победителей ждут дипломы журнала «Квантик», научно-популярные книги.
Конкурс ориентирован на школьников 5-8 классов, но и младшеклассники могут присылать решения. Вносите решения задач VII тура, с которыми справитесь, не позднее 5 апреля в систему проверки konkurs.kvantik.com (инструкция kvantik.com/short/matkonkurs), или высылайте по электронной почте , либо обычной почтой по адресу: 119002, Москва, Б. Власьевский пер., д. 11, журнал «Квантик». В письме кроме имени и фамилии укажите город, школу и класс, в котором вы учитесь, а также обратный адрес.
Задачи и результаты конкурсов прошлых лет: 2024/2025, 2023/2024, 2022/2023, 2021/2022, 2020/2021, 2019/2020, 2018/2019, 2017/2018, 2016/2017, 2016, 2015, 2014, 2013, 2012.
Желаем успеха!
VII тур
Задача 31. (Борис Френкин)
Каждый из троих жителей острова либо правдолюб (всегда говорит правду), либо лжец (всегда лжёт), причём они знают друг о друге, кто из них кто. Когда они сидели вокруг костра, пришёл путешественник и спросил каждого: «Твой сосед справа — правдолюб?» Прозвучали три ответа (в каком-то порядке): «Да», «Нет», «Не знаю». Правдолюб или лжец тот, о ком сказано «Не знаю»?

Задача 32. (Владимир Красноухов)
Пришла пора разобрать ёлку до следующей зимы! Разделите фигуру на рисунке на 6 равных (одинаковых по форме и размерам) частей и сложите из этих частей три зеркально-симметричные ёлочки.
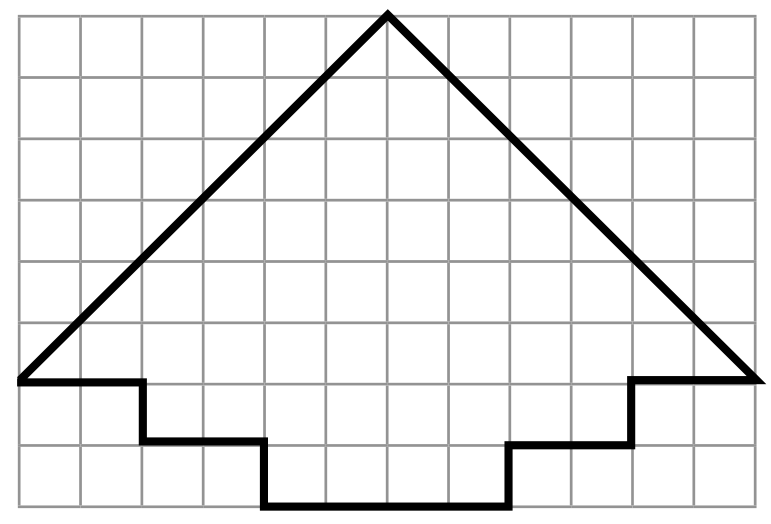

Задача 33. (Михаил Ильинский)
Барон Мюнхгаузен утверждает, что какие две различные правильные дроби с одинаковым знаменателем ни возьми, между ними найдётся правильная дробь (необязательно несократимая) как со знаменателем на 1 меньше, так и со знаменателем на 1 больше. Не ошибается ли барон? (Числители и знаменатели всех дробей положительны.)

Задача 34. (Николай Долбилин)
Квантик выложил на столе 25 тяжёлых одинаковых круглых монет радиуса 5 мм в виде замкнутой цепочки (каждая монета касается двух соседних). Затем он надел на монеты тонкую резинку, идущую по периметру цепочки, и оказалось, что резинка натянута и касается каждой монеты (см. пример на рисунке). На сколько миллиметров растянется резинка, если в цепочку добавить 26-ю монету (так, чтобы по-прежнему каждая монета касалась двух соседних и резинки)?


Задача 35. (Кирилл Белоусов)
Профессор Чайников изобрёл трёхчашечные весы. За одно взвешивание можно положить в чаши по грузу (или ничего не класть), и чаша с самым лёгким грузом поднимется вверх, а две другие чаши одинаково опустятся вниз. (Если самых лёгких грузов несколько, поднимется только один из них (какой угодно), а оставшиеся одинаково опустятся.)
Профессору принесли 179 монет, из них 178 настоящие и весят одинаково, а одна – фальшивая, отличающаяся по весу. Как ему за несколько взвешиваний определить фальшивую монету, если она
а) легче настоящей;
б) тяжелее настоящей?
в) Сможет ли профессор определить фальшивую монету за конечное количество взвешиваний, если неизвестно, легче она или тяжелее настоящей?

VI тур
Задача 26. (Сергей Полозков)
Алиса и Боб поделили между собой все детальки на рисунке, а затем каждый сложил из своих деталек плоскую фигуру (без наложений, поворачивая детали при необходимости). Могли ли у них получиться одинаковые фигуры?
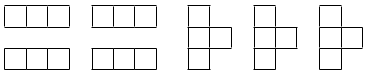

Задача 27. (Борис Френкин)
На двух чашах весов лежит по три монеты, перевешивает левая чаша. Известно, что если выбрать любые две монеты на разных чашах и поменять эти монеты местами, всё равно перевесит левая чаша. Квантик вместо этого поменял местами две монеты левой чаши с двумя монетами правой. Можно ли точно сказать, какая чаша перевесит теперь?

Задача 28. (Георгий Караваев)
У Коли есть три двусторонние карточки, на которых в некотором по- рядке написаны цифры 1, 2, 3, 4, 5 и 7 (на каждой стороне одна цифра). Он сложил из них всевозможные трёхзначные числа и выписал их в список по возрастанию. Семнадцатым в этом списке оказалось число 325. Какое число оказалось в списке пятнадцатым

Задача 29. (Григорий Мерзон)
Оказывается, из 18 копий некоторого пятиугольника можно, не переворачивая их, а только поворачивая, сложить правильный 18-угольник (см. рисунок). Найдите углы этого пятиугольника.
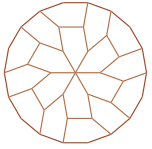

Задача 30. (Георгий Караваев)
За круглым столом сидит 101 человек, каждый из которых является либо рыцарем (всегда говорит правду), либо лжецом (всегда лжёт). Скажем, что справа от человека сидит 50 ближайших его соседей справа, а остальные сидят слева от него. Каждый из сидящих за столом сказал: «Справа от меня сидит больше лжецов, чем слева». Сколько рыцарей могло быть за столом? Найдите все варианты и докажите, что других нет.

V тур
Задача 21. (Дмитрий Калинин)
Разрежьте фигуру на рисунке на 4 равные части.
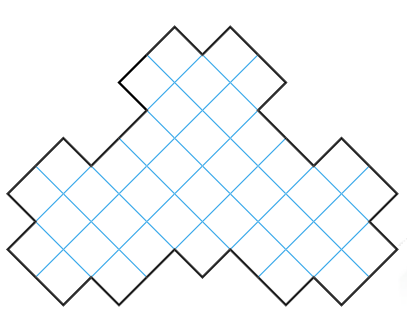

Задача 22. (Сергей Дворянинов)
Незнайка написал по порядку все натуральные числа от 1 до 2026. Сначала он писал их одним цветом, потом другим и, наконец, третьим. Могло ли наименьшее синее число оказаться равным количеству красных чисел, а наибольшее зелёное – количеству синих чисел?

Задача 23. (Игорь Акулич)
Барон Мюнхгаузен заявил: «Можно нарисовать четырёхугольник, у которого две противоположные стороны перпендикулярны, две другие противоположные стороны тоже перпендикулярны, да ещё и диагонали перпендикулярны!» Не ошибается ли барон?

Задача 24. (Татьяна Казицына)
В наборе есть 10 карточек – с числом 1, с числом 2, …, с числом 10. У Васи есть 4 таких набора. Если Вася выложит все 40 карточек в круг, папа даст Васе по одной конфете за каждую пару соседних карточек, разность чисел на которых равна 1 (из большего вычитается меньшее). Какое наибольшее количество конфет может получить Вася? (Приведите пример и докажите, что большее количество конфет Вася получить не сможет.)

Задача 25. (Ольга Манжина)
Есть чашечные весы без гирь и 8 монет; одна из них фальшивая (легче остальных), одна – волшебная (когда она лежит на чаше весов, весы находятся в равновесии). Найдите и фальшивую, и волшебную монеты, потратив всего не более 5 взвешиваний.

IV тур
Задача 16. (Татьяна Казицына)
Пётр, Павел и Панкрат всегда отвечают правду. Фома, Фрол и Филимон всегда отвечают неправду. Например, на вопрос «Твоё имя — Пётр?» четверо ответят «да» и двое ответят «нет». Придумайте простой вопрос, на который один ответит «да» и пятеро ответят «нет».

Задача 17. (Георгий Караваев)
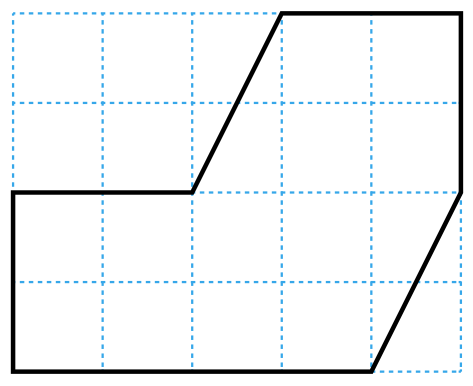
Разрежьте приведённую на рисунке фигуру на 2 равные (по форме и по размеру) части.

Задача 18. (Михаил Евдокимов)
На листе бумаги втайне от вас написали последовательность из 10 натуральных чисел, в которой каждое следующее число, начиная с третьего, равно сумме двух предыдущих. За один вопрос можно узнать сумму любых пяти различных чисел на листе. За какое наименьшее число вопросов можно узнать хотя бы одно записанное число?

Задача 19. (Александр Перепечко)
Барон Мюнхгаузен рассказывал, что однажды подошёл к озеру, на котором росли три лилии. Он бросил три камушка, которые одновременно упали в воду и от каждого по воде пошла одна круговая волна. Барон утверждает, что 1-я лилия колыхнулась по очереди волнами от 1-го, 2-го и 3-го камушков, 2-я лилия — волнами от 2-го, 3-го и 1-го камушков, а 3-я лилия — волнами от 3-го, 1-го и 2-го камушков (именно в таком порядке). Мог ли барон быть прав? (Волны расходятся с одной и той же постоянной скоростью.)

Задача 20. (Георгий Караваев)
Бегун отправился на ежедневную пробежку. Сначала он бежал по тропинке с постоянной скоростью, а потом по асфальтированной дорожке, уже с другой постоянной скоростью. На первую половину пути бегун потратил две трети времени пробежки, а на последние две трети пути он потратил половину времени пробежки. Какую часть дистанции составляет тропинка?

III тур
Задача 11. (Михаил Евдокимов)
Имеются три карточки: с числом ¼, числом 1/3 и числом –1/2. Если в автомат положить три карточки с числами, то через секунду он вернёт их и ещё одну, на которой напечатана сумма чисел на тех трёх карточках. Правда ли, что какое натуральное число ни назови, можно (использовав автомат несколько раз) напечатать карточку с этим числом?

Задача 12. (Борис Френкин)
Готовясь к олимпиаде, Петя и Вася в течение 10 дней решали задачи. В каждый следующий день Петя решал на 1 задачу больше, чем в прошедший, а Вася на 1 задачу меньше. В итоге Вася решил на 90 задач больше, чем Петя. Обязательно ли в какой-то день они решили поровну задач?

Задача 13. (Татьяна Казицына)
Все мыши весили одинаково, а кот весил столько же, сколько все мыши в сумме. Потом мыши съели сколько-то сыра, а после этого кот съел нескольких мышей. И теперь опять кот стал весить столько же, сколько оставшиеся мыши. Мышь может съесть сыра не больше, чем её вес. Докажите, что кот съел не более трети мышей.

Задача 14. (Сергей Шамсутдинов)
Разделите квадрат 3×3 на пять треугольников с различными площадями так, чтобы все вершины треугольников совпадали с вершинами единичных квадратов.

Задача 15. (Александр Грибалко)
Петя взял чётное число трёхклеточных уголков и сложил из них клетчатый прямоугольник (без дырок и наложений). Может ли быть так, что при любом его разрезании на доминошки найдётся уголок, разрезанный на три части?

II тур
Задача 6. (Алексей Толпыго)
Шахматный конь стоит на поле a1 шахматной доски. За какое наименьшее число ходов он может обойти все остальные поля диагонали a1–h8?

Задача 7. (Михаил Евдокимов)
Барон Мюнхгаузен вырезал из бумаги две одинаковые фигуры. Он утверждает, что можно положить их на стол без перекрытий тремя разными способами так, что объединённая фигура в первом случае будет иметь ровно одну ось симметрии, во втором – ровно две, а в третьем – ровно три. Могут ли слова барона оказаться правдой?

Задача 8. (Сергей Костин)
В классе 25 учеников. Могут ли они построиться в виде квадрата 5×5 так, чтобы рядом с каждой девочкой (то есть слева, справа, спереди или сзади от неё) стояло ровно два мальчика, если в классе:
а) 12 девочек и 13 мальчиков;
б) 13 девочек и 12 мальчиков?

Задача 9. (Сергей Костин)
На доске написаны числа (см. рисунок). Квантик рассмотрел всевозможные наборы из трёх различных чисел, написанных на доске. В каждом наборе он перемножил все числа и все эти произведения сложил, получилось число A. Ноутик рассмотрел всевозможные наборы из семи различных чисел, написанных на доске. В каждом наборе он перемножил все числа и все эти произведения сложил, получилось число B. Какое число больше – A или B?
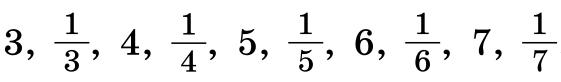

Задача 10. (ученики 10 класса Гусейн Гусейнов и Фарид Мирзелиев)
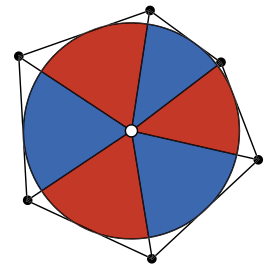
Все стороны шестиугольника касаются круга (см. рисунок). Центр круга соединили отрезками с вершинами шестиугольника, разбив круг на 6 секторов. Эти секторы поочерёдно закрасили в красный и синий цвета. Докажите, что суммарная площадь красных секторов равна суммарной площади синих.

I тур
Задача 1. (Георгий Караваев)
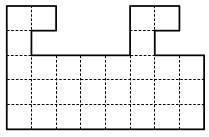
Фигуру на рисунке разрежьте на 2 равные (по форме и по размеру) части.

Задача 2. (Сергей Полозков)
Расставьте в квадратные клеточки на рисунке четыре различные цифры, а в каждый кружочек – различные знаки «+», «–», «•», «:» так, чтобы после выполнения четырёх действий (по стрелкам) получалось одно и то же число (на рисунке оно обозначено буквой x).
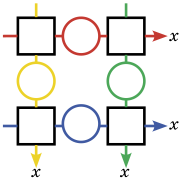

Задача 3. (Игорь Акулич)
Учитель написал на доске пять различных простых чисел. Третьеклассник Вася нашёл сумму трёх из них – получилось 100. Четвероклассник Петя нашёл сумму четырёх из них – получилось 1000. Какова сумма всех пяти чисел?

Задача 4. (Егор Бакаев, Борис Френкин)
Разрежьте закрытую картонную кубическую коробку на две части и сложите из каждой части новую закрытую прямоугольную коробку так, чтобы суммарный объём новых коробок был в два раза меньше объёма исходной коробки. (Резать и сгибать картон можно как угодно, лишь бы итоговые части не разваливались на куски; при складывании картон везде должен быть в один слой.)

Задача 5. (Сергей Костин)
На поле 77×77 каждая клетка синяя или зелёная, причём синих клеток 304. Если в каком-то квадрате 3×3 все клетки, кроме одной, синие, Квантику разрешается перекрасить единственную зелёную клетку тоже в синий цвет.
а) Придумайте такую начальную раскраску, чтобы Квантик, действуя по этому правилу, смог перекрасить всё поле в синий цвет.
б) Удалось бы придумать такую раскраску, если бы синих клеток было 303?


