Математический конкурс 2016 года
Конкурс окончен! Поздравляем победителей!
VIII тур
Задача 36. (Егор Бакаев)
Учительница попросила Васю выписать все целые числа от 1 до 100 в любом порядке. Вася решил выписать их подряд, но поскольку он всегда путает цифры 6 и 9, получилось вот что: 1, 2, 3, 4, 5, 9, 7, 8, 6, 10, 11, 12, 13, 14, 15, 19, 17, …, 67, 68, 66, 100. Выполнил ли Вася задание учительницы?

Задача 37. (Григорий Гальперин)
Обведём в красный кружок каждое число от 1 до миллиарда, у которого все цифры нечётные, а у следующего за ним числа все цифры чётные. Обведём в синий кружок каждое число от 1 до миллиарда, у которого все цифры чётные, а у следующего за ним числа все цифры нечётные. Каких чисел больше — красных или синих, и во сколько раз?
Задача 38. (Григорий Гальперин)
В комнате собралось несколько человек, каждый из которых либо рыцарь, либо лжец (рыцари всегда говорят правду, а лжецы всегда лгут). Затем каждый сказал остальным одно и то же: «Среди вас всего 5 рыцарей и 7 лжецов». И вдруг один из присутствующих сказал: «Мы все солгали». Сколько же всего было человек в комнате, и сколько из них лжецов, а сколько рыцарей?

Задача 39. (Наталия Стрелкова)
Изображённую на рисунке фигуру разрежьте на четыре одинаковые части.
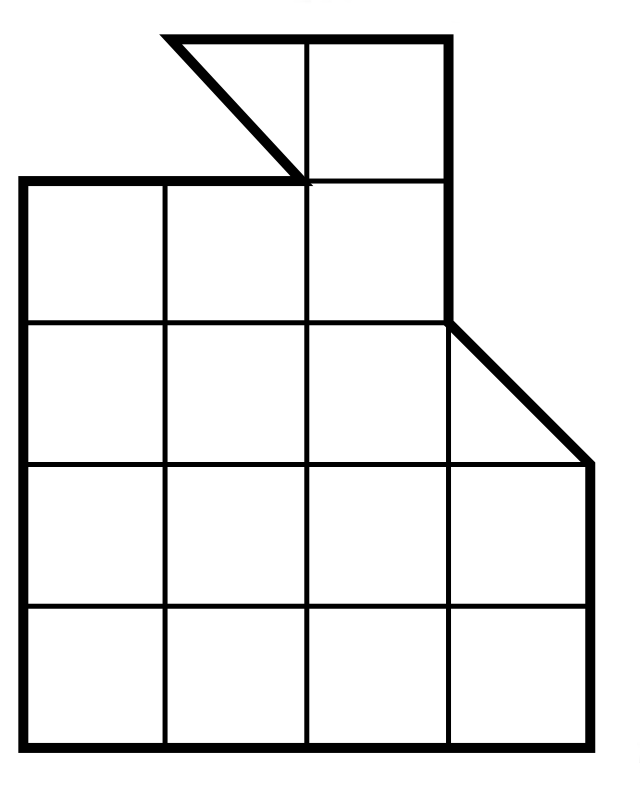
Задача 40. (Павел Кожевников)
а) Дана клетчатая полоска 1x9, клетки которой раскрашены в шахматном порядке. За одну операцию надо выбрать в ней любую одну или несколько подряд идущих клеток и перекрасить их в противоположный цвет. Сделайте полоску одноцветной за 4 операции.
б) А можно ли сделать её одноцветной за 3 операции?
в) Теперь дана доска 9x9, клетки которой раскрашены в шахматном порядке. За одну операцию надо выбрать на доске любой клетчатый прямоугольник и во всех его клетках изменить цвет на противоположный. Сделайте доску одноцветной, потратив всего 8 операций.
г) А можно ли сделать её одноцветной за 7 операций?

VII тур
Задача 31.
Двадцать пять ребят пошли в лес и стали ловить кузнечиков. Несколько ребят поймали по одному кузнечику, половина оставшихся ребят поймали по два кузнечика, а остальные не смогли поймать ни одного. Сколько всего кузнечиков поймали ребята?

Задача 32. (Алексей Воропаев)
а) На рисунке изображена салфетка из 13 клеток. Какое наибольшее количество неперекрывающихся доминошек 1x2 можно уместить на этой салфетке?
б) А какое наименьшее количество доминошек потребуется, чтобы покрыть салфетку целиком, если доминошки могут перекрываться?
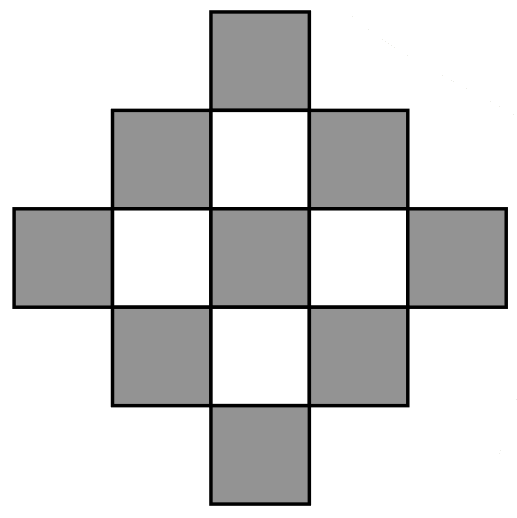

Задача 33. (Андрей Меньщиков)
На доске написаны в ряд четыре четвёрки: 4 4 4 4. Между каждыми двумя соседними четвёрками надо поставить один из знаков «+», «–», «x» или «:», затем расставить скобки (если потребуется) и вычислить значение. Получите таким способом каждую из цифр от 0 до 9.
Задача 34. (Николай Авилов)
Разрежьте какой-нибудь куб на одинаковые кубики и переложите их так, чтобы получилось 49 кубов, не обязательно одного размера.

Задача 35. (Алексей Бирюлин)
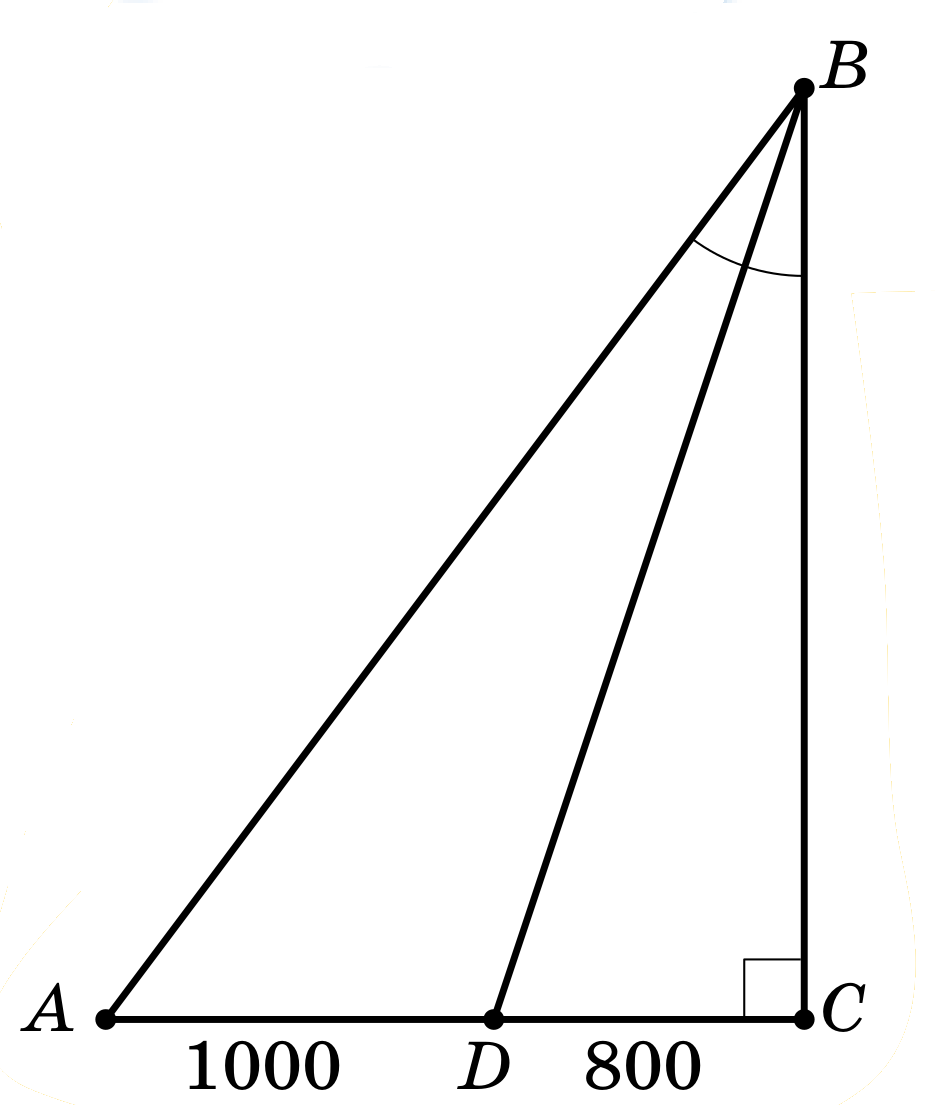
Дорожки парка расположены так, как показано на рисунке: угол ACB прямой, дорожка BD делит угол ABC пополам. Точка B – вход в парк, а точка D – ларёк с мороженым. Буратино и Мальвина решили купить мороженое, но пошёл сильный дождь, и дорожку BD размыло (по ней нельзя пройти), а на дорожке BC образовалась огромная лужа. Поэтому Мальвина пошла по сухой дороге через точку A, а Буратино, любящий лужи, побежал по дороге через точку C. На сколько метров путь Буратино короче пути Мальвины, если AD = 1000 м, а DC = 800 м?

VI тур
Задача 26. (Григорий Гальперин)
За круглым столом сидят десять человек: рыцари и лжецы (и те, и другие присутствуют). Рыцари всегда говорят правду, а лжецы всегда лгут. Каждого спросили, кто сидит справа от него – рыцарь или лжец. Могло ли число ответов «справа от меня сидит лжец» равняться а) двум; б) одному?

Задача 27.
Ноутик нарисовал на плоскости несколько отрезков, которые не пересекаются друг с другом. Всегда ли Квантик сможет соединить некоторые из их концов другими отрезками так, чтобы получилась одна несамопересекающаяся ломаная?

Задача 28. (Андрей Меньщиков)
Найдите какие-нибудь два различных натуральных числа, больших пяти, которые и в сумме, и в произведении дают число-палиндром. (Напомним, что число называется палиндромом, если цифры в нём идут слева направо в том же порядке, что и справа налево, например: 717, 55, 3223.)

Задача 29. (Игорь Акулич)
Если одну из сторон квадрата уменьшить на 4 см, а вторую увеличить на 5 см, площадь получившегося прямоугольника станет меньше площади квадрата. Уменьшится или увеличится площадь, если одну из сторон этого квадрата уменьшить на 1 см, а вторую увеличить на 2 см?
Задача 30. (Александр Романов)
а) Двенадцать ребят решили сыграть в волейбол. На каждую игру тренер разбивает их на две команды по 6 человек. Он хочет провести несколько игр, чтобы в итоге каждый сыграл с каждым в одной команде. Какое наименьшее число игр потребуется?
б) Тут прибежало ещё 10 человек, и ребята решили сыграть в футбол. Теперь тренер разбивает их на две команды по 11 человек и снова хочет провести несколько игр, чтобы в итоге каждый сыграл с каждым в одной футбольной команде. Какое наименьшее число игр потребуется?

V тур
Задача 21.
На одной чашке весов лежат 6 апельсинов, а на другой – 2 дыни. Если добавить одну такую же дыню к апельсинам, то весы уравновесятся. Сколько апельсинов уравновесят дыню?

Задача 22. (Михаил Евдокимов)
Квантик заменил некоторые знаки умножения на знаки сложения и расставил скобки так, что равенство 1·2·3·4·5·6·7·8·9 = 2016 стало верным. А сможете ли вы это сделать?
Задача 23. (Григорий Гальперин)
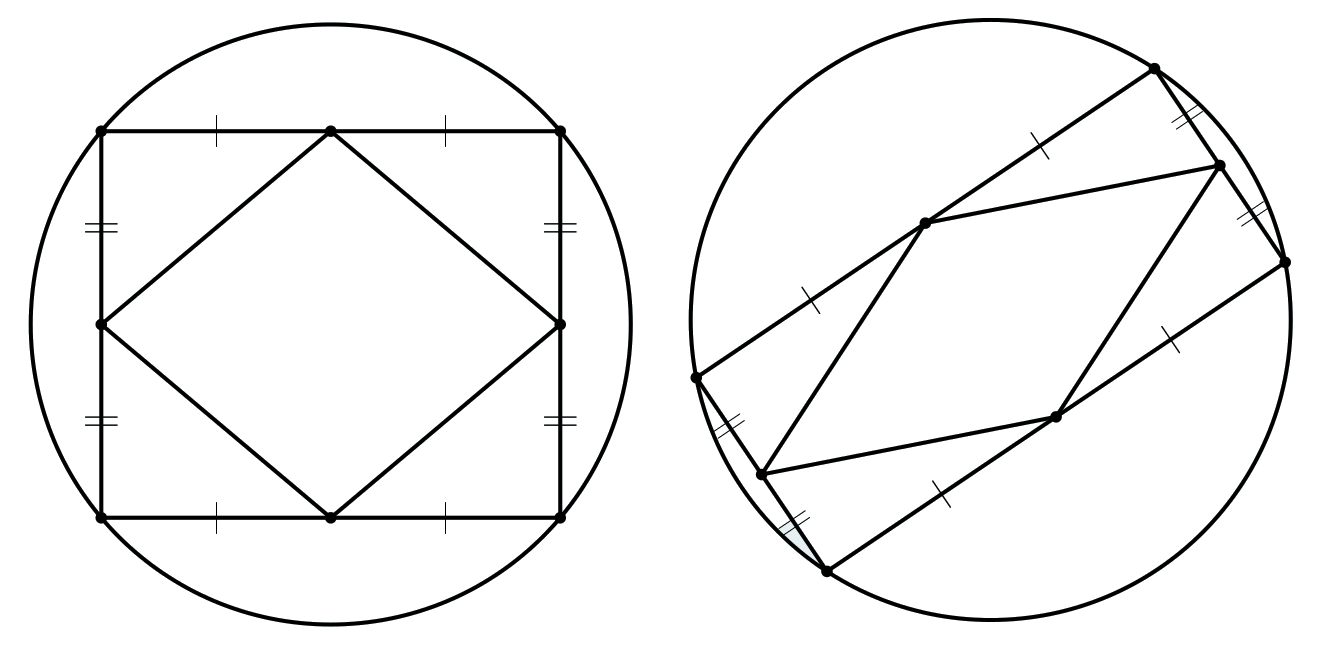
Петя и Вася вписали в круги одного и того же радиуса 5 см по прямоугольнику. Затем каждый из них соединил середины сторон своего прямоугольника и получил ромб (как на рисунке). Докажите, что стороны этих ромбов одинаковы, и найдите их длины.

Задача 24.
В 8 «А» классе усиленно изучают физику, математику и химию. Известно, что не всем любителям математики нравится и физика, а также что всем любителям химии, которым не нравится физика, не нравится и математика. Правда ли, что не всем любителям математики нравится химия?

Задача 25.
Отметьте на листе бумаги 9 точек и проведите 10 прямых так, чтобы на каждой прямой оказалось ровно по три отмеченных точки.

IV тур
Задача 16.
В коробке лежали спички. Их количество удвоили, а затем убрали 8 спичек. Остаток спичек снова удвоили, а затем снова отняли 8 спичек. Когда эту операцию проделали в третий раз, то в коробке не осталось ни одной спички. Сколько их было сначала?

Задача 17.
Прямоугольник разделён двумя отрезками, параллельными его сторонам, на 4 прямоугольника. Площади трёх из этих кусочков равны 4, 8 и 12 см². Найдите площадь четвёртого кусочка (укажите все варианты).

Задача 18. (Григорий Гальперин)
На столе лежит кучка одинаковых с виду монет, одна из которых фальшивая (то ли легче, то ли тяжелее обычной). Барон Мюнхгаузен положил часть монет в карман, оставив на столе не менее двух монет, и заявил, что фальшивая монета осталась на столе. Как проверить слова барона с помощью чашечных весов без гирь, потратив как можно меньше взвешиваний? (Доступны только монеты на столе, на весы можно класть любое число монет. Решение может зависеть от количества оставшихся монет.)

Задача 19. (Егор Бакаев и Алексей Заславский)
Один мудрец заметил: «Наконец настал такой год, что количество зёрен, равное номеру года, можно разложить по клеткам шахматной доски так, чтобы ни на каких двух клетках не было поровну зёрен». В каком году произошла эта история?

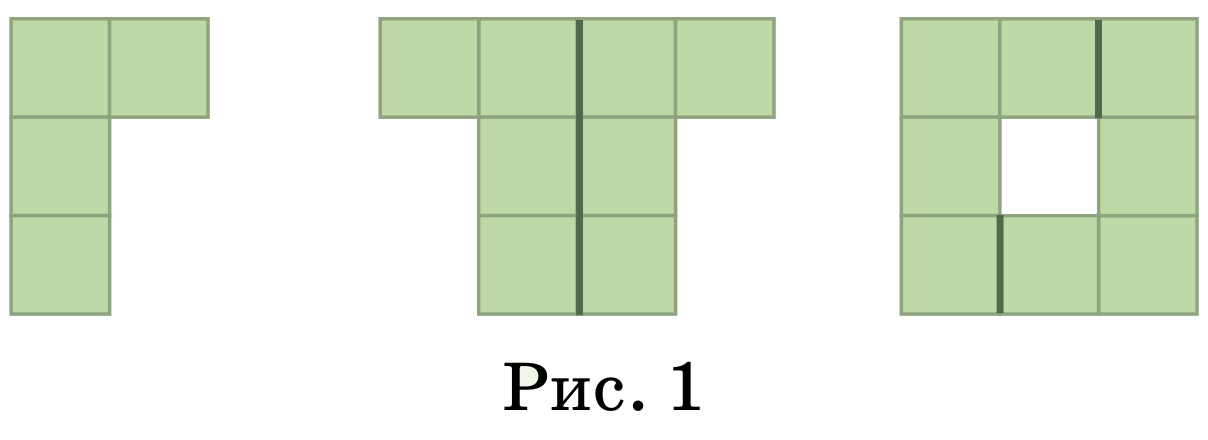
Задача 20. (Николай Авилов)
Квантик рисует в тетради четырёхклеточные буквы «Г» так, чтобы они не накладывались друг на друга. Из двух таких букв «Г» Квантик составил фигуру, имеющую ось симметрии, и даже несколькими способами (см. рисунок 1). Помогите Квантику составить фигуру, имеющую ось симметрии, из любого количества таких букв «Г», большего 2.
III тур
Задача 11.
Когда Петя, Коля, Вася и Дима играли в мяч, один из ребят разбил окно. На вопрос «Кто разбил окно?» все, кроме Димы, ответили «Не я», а Дима ответил «Не знаю». Оказалось, что двое мальчиков сказали правду, а двое соврали. Сказал ли Дима правду?

Задача 12. (Андрей Меньщиков)
Вася получил за год несколько оценок по математике, всего их было меньше 100. Ровно треть из них – тройки, ровно четверть – четвёрки, ровно пятая часть – пятёрки. А сколько Вася получил двоек? Назовите точное количество.

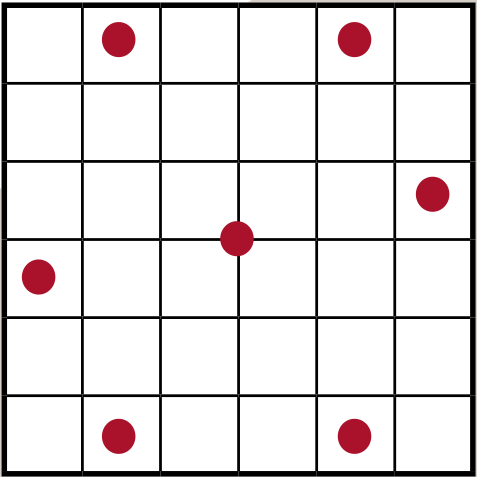
Задача 13. (Михаил Евдокимов)
Белоснежка испекла на праздник торт, разграфлённый на клеточки и украшенный вишенками, как показано на рисунке. Отрезав себе угловую клеточку (правую нижнюю), она хочет разделить оставшуюся часть торта на 7 одинаковых по размеру и форме кусков так, чтобы каждому из семи гномов досталось по целой вишенке. Помогите Белоснежке это сделать.

Задача 14.
На доске в строчку написаны двадцать пятёрок. Поставив между некоторыми из них знак «+», Толя обнаружил, что сумма равна 1000. Сколько плюсов поставил Толя? Укажите все возможные варианты и докажите, что других нет.
Задача 15.
На одной известной картине изображены 4 бурых медведя. Петя и Вася, двое ценителей искусства, по очереди перекрашивают по одному медведю, начинает Петя. Если медведь был бурым, он становится белым, а если был белым – становится бурым. Делая ход, игрок может выбрать любого медведя (в том числе и ранее перекрашенного), но при условии, что после смены цвета картина не станет точно такой же, какой она была в какой-то предыдущий момент. Проигрывает тот, кто не может сделать ход. Кто из игроков может гарантировать себе победу, как бы ни играл его соперник?

II тур
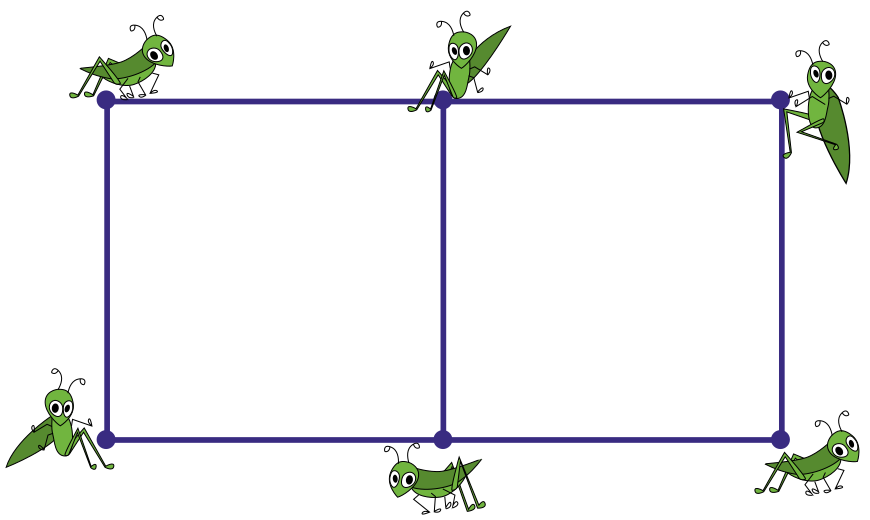
Задача 6. (Николай Авилов)
Шесть кузнечиков сидят в вершинах двух квадратов с общей стороной, как показано на рисунке. Три кузнечика прыгнули каждый на новое место, все прыжки были одинаковой длины. Могли ли после этого все шестеро кузнечиков вновь оказаться в вершинах двух квадратов с общей стороной другого размера?

Задача 7. (Григорий Гальперин)
Рыцари двух кланов собрались в замке на переговоры и расселись в каком-то порядке за большим круглым столом. Оказалось, что рыцарей, справа от которых сидит рыцарь из другого клана, столько же, сколько и рыцарей, справа от которых сидит рыцарь из его же клана. Докажите, что общее число рыцарей делится на 4.

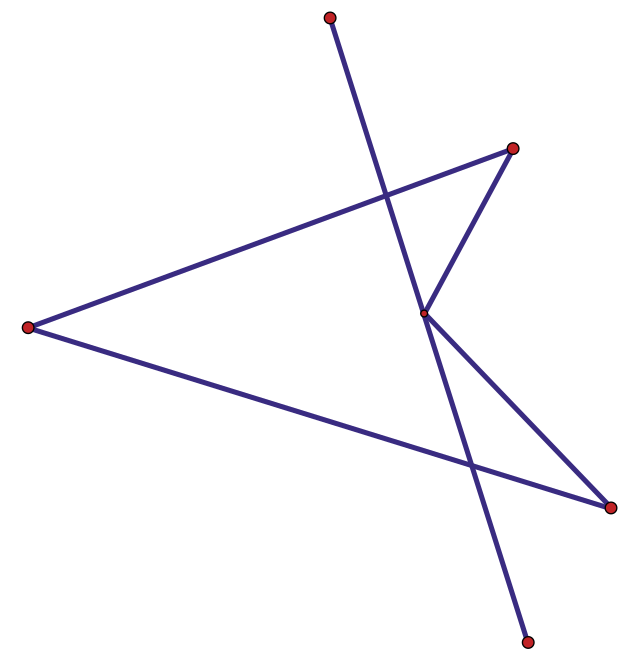
Задача 8. (Дмитрий Шноль)
Четырёхугольник, изображённый на рисунке, можно разрезать одним прямолинейным разрезом на 3 треугольника.
а) Нарисуйте шестиугольник, который можно разрезать одним прямолинейным разрезом на 3 треугольника.
б) Нарисуйте семиугольник, который можно разрезать одним прямолинейным разрезом на 3 треугольника.
в) Сколько углов может быть у многоугольника, если известно, что его можно разрезать одним прямолинейным разрезом на 3 треугольника?
Задача 9. (Игорь Акулич)
Можно ли записать по кругу несколько чисел (не обязательно положительных) так, чтобы среди них не было одинаковых и чтобы каждое число равнялось сумме двух своих соседей?
Задача 10. (Григорий Гальперин)
Одна большая капля ртути и ещё несколько одинаковых маленьких капель на горизонтальной поверхности подтекли друг к другу и слились в одну огромную каплю. Диаметр большой капли в 2 раза больше, чем диаметр каждой из маленьких капель, а диаметр возникшей огромной капли в 5 раз больше диаметра каждой из маленьких капель. Сколько было маленьких капель? Считайте, что все капли строго шарообразные.

I тур
Задача 1. (Григорий Гальперин)
Город разделён рекой на две половины, в каждой половине живёт по миллиону человек. В первый год 2015 человек переселились из левой половины в правую; во второй год 2016 человек переселились из правой половины в левую; в третий год опять 2015 человек переселились слева направо; в четвёртый год – 2016 человек переселились справа налево, и так далее.
Докажите, что в какой-то год в каждой из половин снова окажется по миллиону жителей. Через сколько лет это случится?
Задача 2. (Павел Кожевников)
Барон Мюнxгаузен утверждает, что может нарисовать две пересекающиеся прямые и 15-угольник так, что каждая вершина 15-угольника будет лежать на одной из этих прямых. Не хвастает ли барон?
(Ответ обоснуйте: либо нарисуйте пример, либо докажите, что такого примера нет.)

Задача 3. (Игорь Акулич)
а) Квадратную таблицу размером 3x3 можно разными способами заполнить натуральными числами. Петя и Коля рассматривают суммы чисел по трём строкам, трём столбцам и двум большим диагоналям. Петя убеждён, что если семь из восьми указанных сумм равны между собой, то и восьмая сумма им равна. Коля считает, что не обязательно. Кто прав?
б) Ответьте на тот же вопрос, если квадрат заполнен не просто натуральными числами, а строго числами от 1 до 9 включительно.

Задача 4. (Сергей Дворянинов)
На столе лежит треугольник периметра 10. На стол положили окружность длины 1 так, чтобы она касалась извне одной из сторон треугольника, и прокатили по его контуру, сделав один оборот вокруг треугольника. Какой путь прошёл при этом центр окружности? (Окружность катится без проскальзывания, оставаясь вне треугольника.)

Задача 5.
На доске в ряд написаны 100 произвольных целых чисел, их сумма нечётная. Ноутик и Кватик по очереди забирают себе по числу, но брать можно только число с краю. Начинает Ноутик. Когда каждый наберёт по 50 чисел, игра заканчивается. Тот, у кого сумма чисел окажется больше, выигрывает. Может ли Ноутик действовать так, чтобы всегда выигрывать у Квантика, как бы тот ни сопротивлялся и какие бы числа ни были написаны на доске?

